直列コンデンサによる送電能力の向上

本稿では，長距離送電線の送電容量増大と安定度向上に有効な方法である直列コンデンサについて説明する。

直列コンデンサによる送電能力の向上
送電線への直列コンデンサ設置の事例
直列コンデンサを挿入した三相 3 線式送電系統の損失
参考文献
更新履歴

送電線路において直列コンデンサを設置すると，線路のリアクタンス（インピーダンス）を減少させ，等価的に線路長を減少させる効果を持つ。

このため，長距離送電線に設置すると効果が大きい。

しかし，線路のリアクタンス（インピーダンス）を減少させることは短絡・地絡事故が発生したときの事故電流（故障電流または短絡・地絡電流）の増大につながるため，遮断器容量の問題や直列コンデンサ端子間に過電圧（異常電圧）が発生する問題が生じる。

過電圧（異常電圧）については，端子間に放電ギャップや酸化亜鉛素子を設置し，保護する。

直列コンデンサ設置送電線の負荷側で変圧器を並列した場合には，変圧器鉄心の飽和現象により分数調波振動（鉄共振現象，共振性過電圧）が発生する場合がある。

また，同期機の負制動現象による安定性問題として軸ねじれ現象があるが，この現象は補償度を上げるほど増加する傾向があるので，補償度の上限を決定する要因となる。

送電線への直列コンデンサ設置の事例

送電線への直列コンデンサ設置の事例は，海外ではスウェーデンの 400 kV 系統やアメリカ BPA 500 kV 系統に多数実施例がある。

日本では，1955 年，九州電力の山家変電所に 220 kV 直列コンデンサ設備が初めて設置され，1973 年には関西電力の 275 kV 大黒部幹線（亘長 244 km）に設置されている。

日本の系統は，海外に比較して送電線距離が比較的短いので，直列コンデンサの設置例が少ない。

直列コンデンサを挿入した三相 3 線式送電系統の損失

送電線 1 に直列コンデンサを挿入した図のような三相 3 線式送電系統の送電損失について考える。

なお，送電線 2 と 3 は開閉所を介して接続されている。

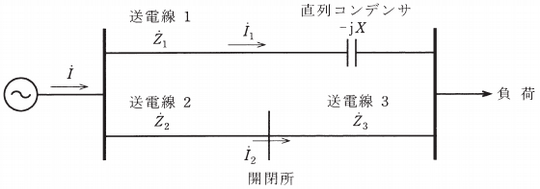
送電線 1 ， 2 を流れる電流の合計 $\dot{I}$ [A]
送電線 1 ， 2 を流れる電流 $\dot{I_1}$ [A]，$\dot{I_2}$ [A]
送電線 1 ， 2 ， 3 の 1 相当たりのインピーダンス
$\dot{Z_1}=2+j4$ [Ω]，$\dot{Z_2}=2+j3$ [Ω]，$\dot{Z_3}=2+j3$ [Ω]
直列コンデンサのインピーダンス $-jX$ [Ω] （ただし，0 < $X$ < 4）

送電損失 [W] （送電線 1 ～ 3 の合計）を，図中の記号及び下記のインピーダンス値を用いて表すと，$\displaystyle 3(2|\dot{I_{1}}|^2+4|\dot{I_{2}}|^2)$ となる。

また，送電線 2 を流れる電流 $\dot{I_2}$ は，$\dot{I}$ と $X$ を用いて表すと，$\displaystyle \frac{\dot{Z_1}-jX}{(\dot{Z_1}-jX)+(\dot{Z_2}+\dot{Z_3})}=\frac{2+j(4-X)}{6+j(10-X)}\dot{I}$ となる。

同様に，送電線 1 の電流 $\dot{I_1}$ を，$\dot{I}$ と $X$ を用いて表し，$|\dot{I_1}|$ と $|\dot{I_2}|$ を $3(2|\dot{I_{1}}|^2+4|\dot{I_{2}}|^2)$ に代入すると，送電損失を $|\dot{I}|$ と $X$ を用いて表すことができる。

この式より，送電損失が最小となるように直列コンデンサのインピーダンスを設定する。

そのときの送電損失 [W] を，$|\dot{I}|$ を用いて表すと $4|\dot{I}|^2$ であることが分かる。