対称座標法の基礎と故障計算：発電機・送電線・変圧器の対称分インピーダンスを体系的に理解する

対称座標法（symmetrical coordinate method）によれば，第一に回転機類も静止器類も送電線路も極めて正しく，かつ簡潔な方法で方程式として表現できる。

第二にこれらを相互接続することが可能であり，したがっていかなる大系統もその計算用回路として構成することができる。

さらに，第三に対称座標法は商用周波数の定常現象・過渡現象はもちろんのこと，高周波現象・サージ現象に至るまであらゆる現象を定量的に扱うことができる。

以上三つの威力を備える対称座標法は電力技術の電気量を扱うあらゆる専門分野で欠くことはできない理論ツールである。

電力系統の故障計算
対称座標法の歴史
- 日本における対称座標法の歴史
参考文献
更新履歴

電力系統の故障計算

電力系統の故障電流は，故障点にテブナンの定理（Thévenin's theorem）を適用し，電力系統側を電圧源とインピーダンスからなる等価回路で表現して計算するのが一般的である。

その際には，故障点に仮想的に設けた端子での三相電圧・電流を対称座標変換し，故障点から見た電力系統を発電機の基本式を用いて表すことにより故障電流を計算することが多い。

対称座標法では，三相（a，b，c で表す）の電圧・電流を零相，正相，逆相（それぞれ 0，1，2 で表す）の電圧・電流に変換する。

例えば正相電流 $\dot{I_1}$ は，三相電流を $\dot{I_\text{a}}$，$\dot{I_\text{b}}$，$\dot{I_\text{c}}$ とすれば，$\displaystyle a = -\frac{1}{2} + \text{j}\frac{\sqrt{3}}{2}$ を用いて $\displaystyle \frac{\dot{I_\text{a}}+a\dot{I_\text{b}} + a^2 \dot{I_\text{c}}}{3}$ となる。

故障前における故障点の a 相電圧を $\dot{E_\text{a}}$，故障点から見た零相，正相，逆相インピーダンスをそれぞれ $\dot{Z_0}$，$\dot{Z_1}$，$\dot{Z_2}$ とするとき，1 線地絡時（故障相は a 相）及び 3 線地絡時の故障点電流は次のとおりとなる。ただし，故障点抵抗は 0 とする。

1 線地絡時 : $\displaystyle \frac{3\dot{E_\text{a}}}{\dot{Z_0}+\dot{Z_1}+\dot{Z_2}}$
1 線地絡時 : $\displaystyle \frac{E_\text{a}}{Z_1}$

上記の計算のためには発電機等の対称分インピーダンスが必要である。

発電機，送電線，変圧器の直列インピーダンスは以下の特徴を有する。

発電機

正相の電機子電流は発電機内に機械的な回転方向と同じ方向に回転する回転磁界を，逆相の電機子電流はそれと反対方向に回転する回転磁界を作るのに対して，零相の電機子電流は発電機内に回転磁界を作らない。

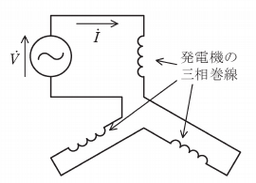
これらにより，発電機の零相，正相，逆相インピーダンスは異なる値をとる。図は，単相の外部電源（電圧 $\dot{V}$）に発電機の三相巻線を直列に接続することにより，発電機の零相インピーダンスを測定する回路である。この場合，$\dot{V}$ は三相電圧の和となるため零相電圧の 3 倍となり，電流 $\dot{I}$ は三相電流が等しいため零相電流だけとなる。このため，$\dot{V}$ と $\dot{I}$ より零相インピーダンスが求められる。

送電線

正相及び逆相電流が作る電線周辺の磁界の大きさはどちらも同じとなるため，正相及び逆相インピーダンスは同一となる。

また，零相インピーダンスは，零相電流が大地を帰路として各相導体に同位相で流れるため，正相，逆相インピーダンスより大きい。

変圧器

正相，逆相インピーダンスとしては変圧器の漏れリアクタンスを考慮する必要がある。また零相インピーダンスには，変圧器の結線方式とともにその中性点接地インピーダンスが大きく影響する。

対称座標法の歴史

対称座標法の発明者は Charles L. Fortescue (1876 - 1936) である。

イギリス生まれであるがアメリカに帰化し，Westinghouse 社の Pittsburgh で特別研究員として活躍した技術者である。

Fortescue は電力機器や絶縁がいしの設計などに携わる一方，コイルインピーダンスの不平衡性に強い関心を抱いてその理論研究に取り組んだ。

その成果として 1918 年に AIEE 論文 "Method of Symmetrical Components Applied to the Solution of Poly-phase Network" を発表する。

Fortescue は，この論文で回転機を含む小さい 3 相回路で 3 相電圧を $E$，$aE$，$a^2 E$ の成分に分解する計算手法を示して，それによって得られる三つの回路に positive-，negative-，zero-sequence circuits の名前を付した。

日本における対称座標法の歴史

対称座標法を再び論文で取り上げた最初の人は日本の別宮貞俊博士である。

同博士は送電線の地絡事故解析の手段として対称座標法の価値を見いだし，下記の論文を発表している。

接地リアクトルについて（別宮貞俊，電気学会誌 1922 年 2 月号）
Calculation of Short-circuit ground currents on three phase power networks using the symmetrical coordinates (S. Bekku, General Electric Review, Vol. 28, 1925)(Elektr Z, 1925)
対称座標法とその送電線問題における応用（電気学会誌 1925 年 11 月号）

また，対称座標法に関する世界最初に出版された著書は別宮博士による "対称座標法解説（1928 年オーム社）" である。