同期発電機の特性曲線

本稿では，同期発電機（synchronous generator）の特性曲線について説明する。

無負荷飽和曲線（no-load saturation curve）

同期発電機を定格回転速度，無負荷で運転している場合の界磁電流に対する端子電圧の関係を示す曲線を無負荷飽和曲線という。

界磁電流の増加に伴い鉄心が飽和するため，界磁電流と端子電圧の関係は比例関係にならず，いわゆる飽和特性を示す曲線になる。

原点において，曲線 OM に接線 OG を引くと，OG はギャップに要する起電力（電流値で表されている）と誘導起電力の関係を示す（いわゆるギャップ線である）。

電圧 $V$ を誘導するのに必要な起電力は，図において $(a+b)$ であって，$a$ および $b$ は，それぞれギャップおよび鉄部分に磁束を通すために必要な起磁力である。

磁気回路の飽和が大きいほど，$b$ が大きくなる。

$b$ と $a$ との比をもって飽和の程度を表すことができ，σ $= b/a$ を飽和係数（saturation factor）という。

図　無負荷飽和曲線

飽和特性（saturation characteristic）

飽和特性（saturation characteristic）とは，規定された負荷，速度などの条件下で，界磁電流と誘導起電力の関係を示す特性である。

無負荷飽和特性（open-circuit characteristic no-load characteristic）

無負荷飽和特性（open-circuit characteristic no-load characteristic）とは，電機子巻線開路状態での回転機の飽和特性である。

図は，三相同期発電機の界磁電流 $I_\text{f}$ に対する 1 相分の無負荷誘導起電力 $E_0$ 及び三相短絡電流 $I_\text{S}$ の特性である。無負荷誘導起電力 $E_0$ と界磁電流 $I_\text{f}$ との間の関係は，

\[ E_0 = \frac{\omega M I_\text{f}}{\sqrt{2}} \]

で与えられる。

ただし，$\omega$ は電気角速度，$M$ は界磁巻線と電機子巻線 1 相との間の相互インダクタンスである。

しかし，実際の無負荷誘導起電力には，図中の $E_0$ のように飽和特性を生じる。

これは，相互インダクタンス $M$ の非線形性に起因するもので，界磁電流の増加に伴って透磁率が減少することにより生じる。

一般に，定格電圧 $V_\text{n}$ を得るための界磁電流 $I_\text{fn}$ は，飽和特性を考慮しない場合の界磁電流 ${I_\text{fn}}'$ に比べて 5 ～ 15 [%] 程度大きい。

図　三相同期発電機の界磁電流に対する 1 相分の無負荷誘導起電力及び三相短絡電流の特性

短絡特性曲線（short-circuit curve）

同期発電機の端子を短絡し，定格回転速度で運転した場合の，界磁電流に対する電機子電流の関係を示す曲線を短絡特性曲線という。

端子短絡状態では，電機子反作用による減磁作用で界磁起磁力の大部分が打ち消されるため界磁電流を増加させても鉄心は磁気飽和せず，特性曲線はほぼ直線となる。

無負荷飽和曲線と短絡特性曲線が得られると，同期発電機の短絡比を求めることができ，この短絡比 $K$ と単位法（p.u.）で表した同期インピーダンスは互いに逆数の関係になる。

短絡特性（short-circuit characteristic）

短絡特性（short-circuit characteristic）とは，同期機の電機子巻線の全端子を短絡し定格回転速度で運転した場合の界磁電流と電機子巻線に流れる短絡電流との関係を示す特性である。

三相短絡電流は界磁電流にほぼ比例し，通常の界磁電流の範囲では，飽和特性の影響は現れない。

これは，電機子電流の減磁作用によるものである。同期リアクタンス $X_\text{S}$ 及び巻線抵抗 $r$ を用いると，三相短絡電流は，$\dot{I}_\text{S} =$ $\displaystyle \frac{E_0}{r+\text{j}X_\text{S}}$ である。

この式を電機子巻線 1 相の自己インダクタンス $L_0$ 及び漏れインダクタンス $l$ で書き換えると，

\[ \dot{I}_\text{S}=\frac{\frac{\omega M I_\text{f}}{\sqrt{2}}}{r+\text{j}\omega(\frac{3}{2}L_0 + l)} \]

となる。

界磁電流による磁束鎖交数は $\displaystyle \frac{MI_\text{f}}{\sqrt{2}}$，短絡電流による磁束鎖交数は $\displaystyle \frac{3}{2}L_0 I_\text{S}$ であるので，界磁及び電機子の漏れインダクタンスと巻線抵抗とを無視すると，

\[ I_\text{S}=\frac{\sqrt{2}}{3}KI_\text{f} \]

となる。

ただし，$K$ は界磁巻線の電機子巻線に対する巻数比である。

上式には，$M$ や $L_0$ などの磁気的に非線形な係数を含まないので，界磁電流 $I_\text{f}$ と三相短絡電流 $I_\text{S}$ とは比例関係になる。

三相同期電動機の短絡比

同期機の特性を示すパラメータの一つに短絡比がある。

短絡比 $K$ とは，定格速度において，無負荷で定格電圧を発生するのに必要な界磁電流（すなわち定格電流 $I_\text{N}$）と，三相短絡の場合に定格電流に等しい短絡電流を発生するのに必要な界磁電流（すなわち短絡電流 $I_\text{N}$）との比である。

\[K=\frac{I_\text{S}}{I_\text{N}}\]

短絡比が大きい機械は，同期インピーダンスが小さいので電機子反作用の影響が小さい機械である。

このような機械とするには，電機子巻線の巻数を少なくするか，ギャップの長さを大きくするか又は両方である。

この場合，一定の誘導起電力を得るには，磁束を増すため界磁起磁力を増やすか又は鉄心断面積を増加させることになり，いずれの場合でも，機械の寸法が大きくなる。

所要巻線量（銅量）はほぼ寸法に比例し，所要鉄量は寸法の 3 乗に比例する。

したがって，短絡比の大きい機械は鉄機械といわれ，電圧変動率が小さく，過負荷耐量も大きく，高価である。

負荷飽和曲線（load saturation curve）

同期発電機を定格回転速度で運転し，電機子電流一定で力率一定の負荷をかけた場合の界磁電流に対する端子電圧の関係を示す曲線を負荷飽和曲線という。

負荷飽和曲線のなかで特に電機子電流値が定格で零力率の負荷をかけた場合の曲線を零力率飽和曲線といい，無負荷飽和曲線をポーシェの三角形を用いて平行移動することでもこの飽和曲線を描くことができる。

負荷飽和特性（load characteristic）

負荷飽和特性（load characteristic）とは，ある負荷条件下での回転機の飽和特性である。

演習問題

令和3年度 第一種 電気主任技術者 一次試験 機械 問1

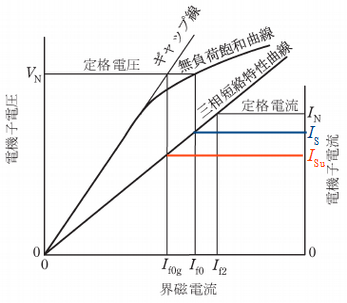
16 000 kV·A，11 000 V の定格を持つ三相同期発電機（以下，試験機と呼ぶ）の試験結果は以下のとおりであった。また，試験結果をグラフ化すると図のようになった。

(a) 無負荷飽和特性試験

端子電圧（線間電圧） [V]	4 000	8 000	11 000	14 300
界磁電流 [A]	205	410	680	1 400

(b) 三相短絡特性試験（定常短絡試験）

電機子電流 [A]	400	600	840
界磁電流 [A]	435	652	913

一般的に同期機には磁気飽和特性があるため，同期リアクタンスには飽和値と不飽和値が定義される。試験機の同期リアクタンスの飽和値 $X_\text{s}$ [%] は，134 % であり，これを Ω 値で表した毎相の同期リアクタンスの飽和値 $X_\text{s}$ [Ω] は，10.2 Ω である。

試験機の同期リアクタンスの不飽和値 $X_\text{su}$ [%] は，図中の記号を用いて $X_\text{su}$ [%] = $X_\text{s}$ [%] × $\displaystyle \frac{I_\text{f0}}{I_\text{f0g}}$ として求められ，試験機の $X_\text{su}$ [%] は，162 % である。

定格電圧における同期機の磁気飽和の程度を表す飽和率 σ は，図中の記号を用いて σ = $(I_\text{f0}-I_\text{f0g})$/$I_\text{f0g}$ として求められる。

図　三相同期発電機の無負荷飽和曲線と三相短絡特性曲線

参考文献

• 電気専門用語集（WEB 版）
• 令和4年度 第二種 電気主任技術者 二次試験 機械・制御 問1「同期発電機」
• 令和3年度 第一種 電気主任技術者 一次試験 機械 問1「三相同期発電機の試験結果」
• 令和元年度 第二種 電気主任技術者 一次試験 機械 問2「同期発電機の特性曲線」
• 平成25年度 第一種 電気主任技術者 一次試験 機械 問1「同期発電機の無負荷飽和曲線と短絡特性曲線」
• 平成18年度 第二種 電気主任技術者 一次試験 機械 問2「三相同期発電機の短絡比」

同期発電機の理論とモデル化

JEC-2130 同期機 [ 電気学会電気規格調査会 ]

更新履歴

• 2022年1月19日　新規作成
• 2022年2月11日　参考文献に「平成18年度第二種 電気主任技術者 一次試験 機械 問2」を追加
• 2022年5月13日　参考文献に「電気専門用語集（WEB 版）」を追加
• 2022年5月14日　無負荷飽和曲線の図を追加
• 2022年5月16日　飽和係数の説明を追加
• 2022年6月18日　参考文献に「令和3年度 第一種 電気主任技術者 一次試験 機械 問1」を追加
• 2022年7月3日　参考文献に「平成25年度 第一種 電気主任技術者 一次試験 機械 問1」を追加
• 2022年7月21日　加除修正
• 2022年7月30日　参考文献の過去問題の題目を追記
• 2022年8月13日　クリエを参考にリライト
• 2023年1月15日　短絡比の定義式を追加，参考文献に「令和4年度 第二種 電気主任技術者 二次試験 機械・制御 問1」を追加
• 2024年1月27日　検索エンジン向けタイトル「同期発電機の特性曲線とは？」，SNS 向けタイトル「同期発電機の特性曲線を解説！無負荷飽和や短絡特性についても #発電機 #特性曲線」を追加（AI タイトルアシストを活用）